Casio fx-5800P - Manual (Página 67)

S-66
A Transponiendo una matriz
La transposición de una matriz signifi ca básicamente que sus fi las se convierten en
columnas y sus columnas en fi las. El cálculo se realiza usando la función Trn( mostrada
debajo.
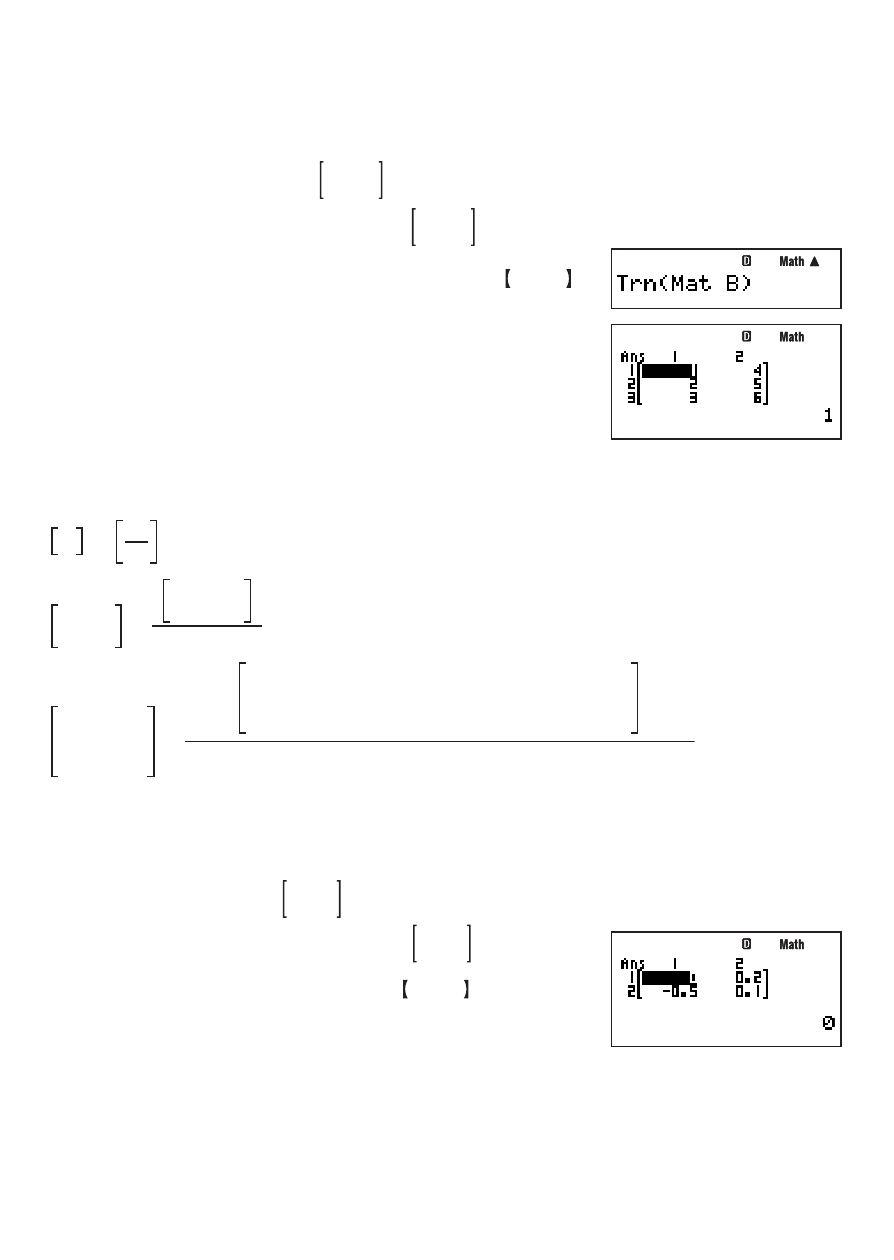
Ejemplo: Transponer la matriz
1 2 3
4 5 6
.
Este ejemplo supone que Mat B contiene
1 2 3
4 5 6
.
z – {MATRIX}4(Trn)
Mat B
)
E
A Invirtiendo una matriz
Puede usar el procedimiento mostrado debajo para invertir una matriz cuadrada.
a
11
–1
=
a
11
1
a
11
a
12
–1
a
21
a
22
a
22
– a
12
– a
21
a
11
a
11
a
22
– a
12
a
21
=
a
11
a
12
a
13
–1
a
21
a
22
a
23
a
31
a
32
a
33
=
a
22
a
33
– a
23
a
32
– a
12
a
33
+ a
13
a
32
a
12
a
23
– a
13
a
22
– a
21
a
33
+ a
23
a
31
a
11
a
33
– a
13
a
31
– a
11
a
23
+ a
13
a
21
a
21
a
32
– a
22
a
31
– a
11
a
32
+ a
12
a
31
a
11
a
22
– a
12
a
21
a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
– a
13
a
22
a
31
– a
12
a
21
a
33
– a
11
a
23
a
32
¡Importante!
• Solamente pueden invertirse las matrices cuadradas con un valor que no sea cero.
• Utilice la tecla
!)( x –1
) para introducir “
–1
”.
Ejemplo: Invertir la matriz
1 –2
5 0
.
Este ejemplo supone que Mat C contiene
1 –2
5 0
.
Mat C
!)( x –1
)
E
A Elevando una matriz al cuadrado
Puede usar el procedimiento mostrado debajo para elevar una matriz al cuadrado.
¡Importante!
Utilice la tecla
x para especifi car la operación de elevación al cuadrado.