Casio CFX-9850GB PLUS Capítulo 3 - Manual (Página 6)

58
3-3 Cálculos diferenciales cuadráticos
Luego de visualizar el menú de análisis de función, puede ingresar expresiones
diferenciales cuadráticas usando uno de los dos siguientes formatos.
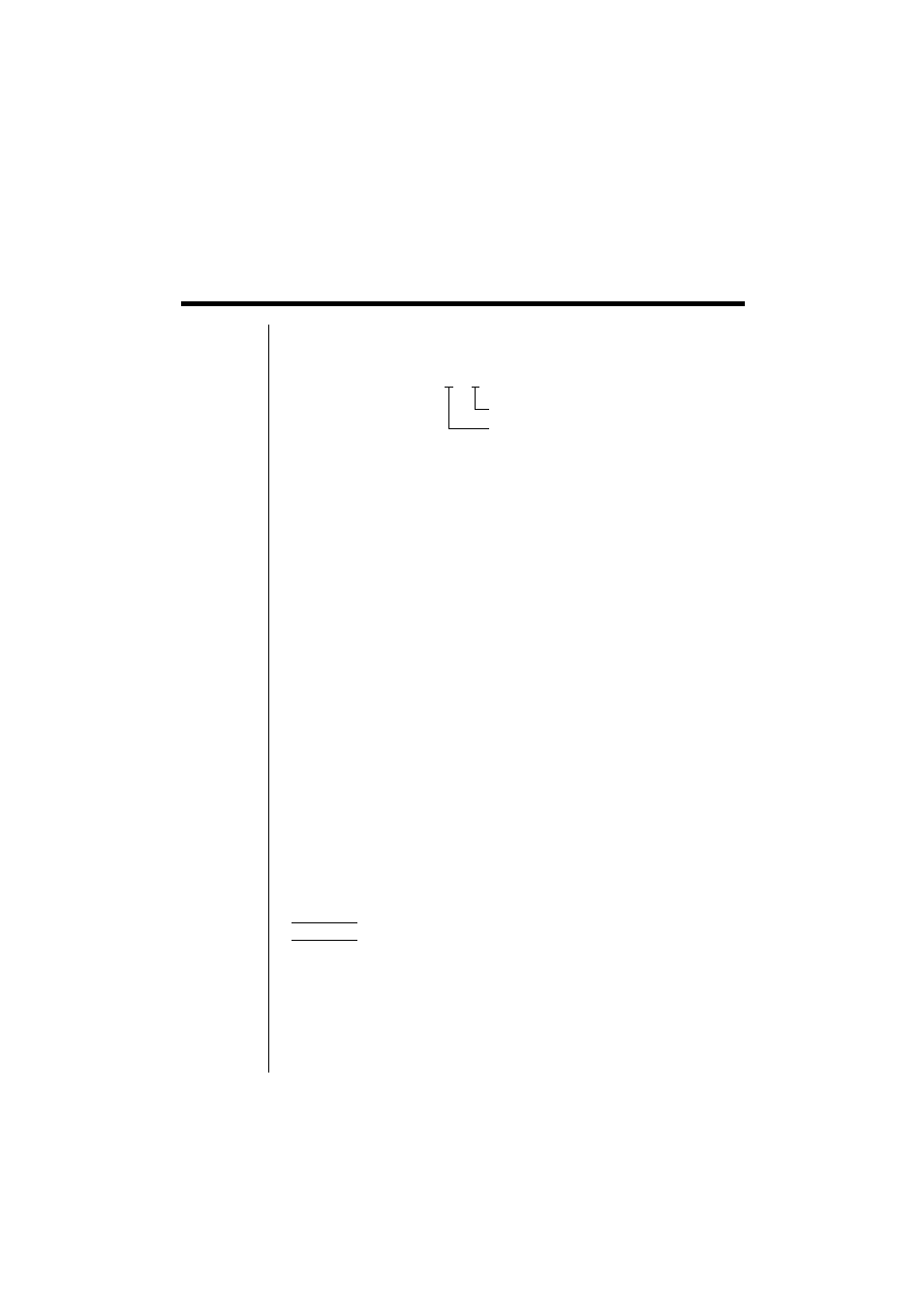
3( d 2 / dx 2 ) f(x) , a , n )
Los cálculos diferenciales cuadráticos producen un valor diferencial aproximado
usando la siguiente fórmula diferencial de segundo orden, que se basa en la
interpretación polinómica de Newton.
– f (x – 2h) + 16 f(x – h) – 30 f (x) + 16 f(x + h) – f(x + 2h)
f''(x) = –––––––––––––––––––––––––––––––––––––––––––––––
12h 2
En esta expresión, los valores para los “incrementos suficientemente pequeños
de
x ” son calculados secuencialmente usando la fórmula siguiente, con el valor
de m siendo sustituido como m = 1, 2, 3 y así sucesivamente.
1
h = ––––
5 m
El cálculo es finalizado cuando el valor de f " (x) basado en el valor de h que se
calcula usando el último valor de m , y el valor de f " (x) basado en el valor de h
que se calcula usando el valor actual de m son idénticos, antes de que se alcance
el límite superior n .
• Normalmente, no se debe ingresar un valor para n . Se recomienda que
solamente ingrese un valor para n cuando se requiera para la precisión del
cálculo.
• Ingresando un valor mayor para n , no necesariamente produce una mayor
precisión.
uuuuu Para realizar un cálculo diferencial cuadrático
Ejemplo Determinar el coeficiente diferencial cuadrático en el punto en
donde
x = 3 para la función y = x 3 + 4 x 2 + x – 6.
En este caso, usaremos un valor de límite final de n = 6.
Ingrese la función f ( x ) .
AK4 (CALC) 3 ( d 2 / dx 2 ) v Md+
evx+v-g,
[OPTN]-[CALC]-[ d 2 / dx 2 ]
d 2 d 2
––– ( f (x), a, n)
⇒ ––– f (a)
dx 2 dx 2
Límite final ( n = 1 a 15)
Punto de coeficiente diferencial